Embark on an advanced journey with our Intermediate Algebra (IA) section, also known as Algebra 2. Delve into intricate topics, unravel complex equations, and enhance your mathematical prowess. Our meticulously crafted resources, combined with illustrative video tutorials, ensure a deeper understanding of algebraic concepts, bridging the gap between foundational knowledge and advanced applications. Whether you're gearing up for a challenging exam or simply eager to expand your algebraic horizons, our Intermediate Algebra section is tailored to meet your needs.
Showing posts with label algebra 2. Show all posts
Showing posts with label algebra 2. Show all posts
Free Algebra Study Guide with Videos
Welcome to OpenAlgebra.com, your comprehensive online destination for mastering algebra. Dive deep into our extensive collection of step-by-step tutorials, complemented by illustrative YouTube videos for a visual learning experience. Whether you're a student seeking supplemental material beyond your textbooks or a teacher looking for a rich resource of worked-out math problems, our platform offers a treasure trove of algebraic knowledge tailored to enhance your understanding.
Embark on an advanced journey with our Intermediate Algebra (IA) section, also known as Algebra 2. Delve into intricate topics, unravel complex equations, and enhance your mathematical prowess. Our meticulously crafted resources, combined with illustrative video tutorials, ensure a deeper understanding of algebraic concepts, bridging the gap between foundational knowledge and advanced applications. Whether you're gearing up for a challenging exam or simply eager to expand your algebraic horizons, our Intermediate Algebra section is tailored to meet your needs.
Embark on an advanced journey with our Intermediate Algebra (IA) section, also known as Algebra 2. Delve into intricate topics, unravel complex equations, and enhance your mathematical prowess. Our meticulously crafted resources, combined with illustrative video tutorials, ensure a deeper understanding of algebraic concepts, bridging the gap between foundational knowledge and advanced applications. Whether you're gearing up for a challenging exam or simply eager to expand your algebraic horizons, our Intermediate Algebra section is tailored to meet your needs.
Solving Exponential Equations
In this section, we will make use of what we have learned about exponential functions to solve equations.
Make use of the above property if you are able to express both sides of the equation in terms of the same base.
Step 1: Express both sides in terms of the same base.
Step 2: Equate the exponents.
Step 3: Solve the resulting equation.
Solve.
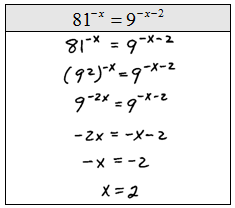
Make use of the above property if you are unable to express both sides of the equation in terms of the same base.
Step 1: Isolate the exponential and then apply the logarithm to both sides.
Step 2: Apply the power rule for logarithms and write the exponent as a factor of the base.
Step 3: Solve the resulting equation.
Solve.
When solving exponential equations and using the above process, the rule of thumb is to choose the common logarithm unless the equation involves the natural base e. We choose these because there is a button for them on the calculator. However, we could certainly choose any base that we wish; this is the basis for the derivation of the change of base formula.
YouTube Videos:
Step 1: Express both sides in terms of the same base.
Step 2: Equate the exponents.
Step 3: Solve the resulting equation.
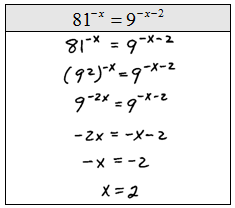
It is not always the case that we will be able to express both sides of an equation in terms of the same base. For this reason we will make use of the following property.
Step 1: Isolate the exponential and then apply the logarithm to both sides.
Step 2: Apply the power rule for logarithms and write the exponent as a factor of the base.
Step 3: Solve the resulting equation.
YouTube Videos:
Properties of the Logarithm
The following properties of the logarithm are derived from the rules of exponents.
The properties that follow below are derived from the fact that the logarithm is defined as the inverse of the corresponding exponential.
To familiarize ourselves with the properties we will first expand the following logarithms. (Assume all variables are positive.)
Expand.
Notice that there is no explicit property that allows us to work with nth roots within the argument of the logarithm. To simplify these, first change the root to a rational exponent then apply the power rule.
When expanding, notice that we must use the same base throughout the expression. For the next set of problems we will first use the properties to expand then substitute in the appropriate values as the last step.
Evaluate
Tip: When simplifying these down to one logarithm use only one operation at a time and work from left to right. Combining or skipping steps usually leads to mistakes. Do not race, work slowly, and pay attention to notation.
Evaluate (Round to the nearest ten thousandths where appropriate).
YouTube Videos:
To familiarize ourselves with the properties we will first expand the following logarithms. (Assume all variables are positive.)
Expand.
Evaluate
Expanding is useful for learning the rules and properties associated with logarithms but as it turns out, in practice, condensing down to a single logarithm is the skill that we really need to focus on.
Rewrite as a single logarithm (condense).
Simplify.
YouTube Videos:
Subscribe to:
Posts (Atom)