Graph using Intercepts

You might be familiar with the basic fact that two points determine a line.  This fact leads to a nice and easy way to graph lines using the two points called the x- and y-intercepts.

All x-intercepts, if they exist, must have a corresponding y-value of zero.  All y-intercepts must have a corresponding x-value of zero.  This might sound confusing but just remember the following steps to algebraically find intercepts.

Example: Graph 3x − 5y = 15 using the x- and y-intercepts.

Plot the points and draw a line through them with a straight edge.

Instructional Video: Graphing by Finding Intercepts

This is a nice and easy method for determining the two points you need for graphing a line.  In fact, we will use this exact technique for finding intercepts when we study the graphs of all the conic sections later in our study of Algebra.  Be careful not to say that y = −3 is the y-intercept because the intercepts, actually, are ordered pairs or points on the graph so you should take care to say (0,−3) is the y-intercept.

Use the given graph to answer the question.

  

Be sure to pay attention to the scale. Misreading the scale is the most common error in this type of problem.
  

Example: Graph −4x + 3y = 12 using the intercepts.

             

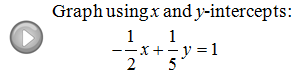
Example: Graph −4x + 2y = −6 using the intercepts.

              

Example: Graph y = −5x +15 using the intercepts.

               

Example: Graph y = −3/4 x + 9 using the intercepts.

                 

This brings us to one of the most popular questions in linear graphing.  Do all lines have x- and y-intercepts?  The answer is NO.  Horizontal lines, of the form y = b, do not necessarily have x-intercepts.  Vertical lines, of the form x = a, do not necessarily have y-intercepts.

Example: Graph y = 3.

           

Example: Graph x = −2.

        

Instructional Video: Graphing Horizontal and Vertical Lines

Video Examples on YouTube:  Graphing Linear Functions Playlist









---