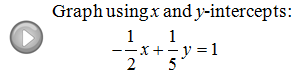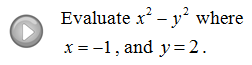Embark on an advanced journey with our Intermediate Algebra (IA) section, also known as Algebra 2. Delve into intricate topics, unravel complex equations, and enhance your mathematical prowess. Our meticulously crafted resources, combined with illustrative video tutorials, ensure a deeper understanding of algebraic concepts, bridging the gap between foundational knowledge and advanced applications. Whether you're gearing up for a challenging exam or simply eager to expand your algebraic horizons, our Intermediate Algebra section is tailored to meet your needs.
OpenAlgebra.com
Free Algebra Study Guide with Videos
Embark on an advanced journey with our Intermediate Algebra (IA) section, also known as Algebra 2. Delve into intricate topics, unravel complex equations, and enhance your mathematical prowess. Our meticulously crafted resources, combined with illustrative video tutorials, ensure a deeper understanding of algebraic concepts, bridging the gap between foundational knowledge and advanced applications. Whether you're gearing up for a challenging exam or simply eager to expand your algebraic horizons, our Intermediate Algebra section is tailored to meet your needs.
Factoring Lesson C by ChatGPT-4
Factoring Trinomials of the Form \(x^2 - bx - c\)
Factoring trinomials, which are polynomials with three terms, can initially seem challenging. However, with practice, it becomes routine. If a trinomial factors, it will factor into the product of two binomials.
Steps to Factor Trinomials:
- Factor the first term: \(x^2 = x \cdot x\).
- Factor the last term: Choose factors that multiply to obtain the last term and subtract to obtain the middle term.
- Determine the signs: by adding or subtracting the product of the inner and outer terms.
- Check by multiplying.
Example:
Factor the trinomial \(x^2 - 3x - 10\).
- Factor the first term: \(x^2 = x \cdot x\).
- Factor the last term: \(-10 = -5 \cdot 2\) and \(-5 + 2 = -3\), which is our middle term.
- Determine the signs: One sign is positive and the other is negative because \(-5 + 2 = -3\).
- Check by multiplying: \((x - 5)(x + 2) = x^2 - 3x - 10\).
So, \(x^2 - 3x - 10 = (x - 5)(x + 2)\).
Exercises:
Factor the following trinomials:
- \(x^2 - 5x - 6\)
- \(x^2 - 7x + 10\)
- \(x^2 - 6x - 16\)
- \(x^2 - 8x - 9\)
- \(x^2 - 3x - 10\)
- \(x^2 - 4x - 21\)
- \(x^2 - 5x - 14\)
- \(x^2 - 6x - 16\)
- \(x^2 - 7x - 18\)
- \(x^2 - 9x - 22\)
Solutions:
- \(x^2 - 5x - 6 = (x - 6)(x + 1)\)
- \(x^2 - 7x + 10 = (x - 2)(x - 5)\)
- \(x^2 - 6x - 16 = (x - 8)(x + 2)\)
- \(x^2 - 8x - 9 = (x - 9)(x + 1)\)
- \(x^2 - 3x - 10 = (x - 5)(x + 2)\)
- \(x^2 - 4x - 21 = (x - 7)(x + 3)\)
- \(x^2 - 5x - 14 = (x - 7)(x + 2)\)
- \(x^2 - 6x - 16 = (x - 8)(x + 2)\)
- \(x^2 - 7x - 18 = (x - 9)(x + 2)\)
- \(x^2 - 9x - 22 = (x - 11)(x + 2)\)
Remember to always check your results by multiplying the factors. If the product matches the original trinomial, then the factoring is correct.
Factoring Lesson B by ChatGPT-4
Factoring Trinomials of the Form \(x^2 - bx + c\)
Factoring trinomials, which are polynomials with three terms, can initially seem challenging. However, with practice, it becomes routine. If a trinomial factors, it will factor into the product of two binomials.
Steps to Factor Trinomials:
- Factor the first term: \(x^2 = x \cdot x\).
- Factor the last term: Choose factors that multiply to obtain the last term and add to obtain the middle term.
- Determine the signs: by adding or subtracting the product of the inner and outer terms.
- Check by multiplying.
Example:
Factor the trinomial \(x^2 - 7x + 10\).
- Factor the first term: \(x^2 = x \cdot x\).
- Factor the last term: \(10 = 5 \cdot 2\) and \(5 + 2 = 7\), which is our middle term.
- Determine the signs: Both signs are negative because \(-5 - 2 = -7\).
- Check by multiplying: \((x - 5)(x - 2) = x^2 - 7x + 10\).
So, \(x^2 - 7x + 10 = (x - 5)(x - 2)\).
Exercises:
Factor the following trinomials:
- \(x^2 - 5x + 6\)
- \(x^2 - 9x + 20\)
- \(x^2 - 7x + 10\)
- \(x^2 - 11x + 30\)
- \(x^2 - 8x + 15\)
- \(x^2 - 10x + 21\)
- \(x^2 - 6x + 8\)
- \(x^2 - 12x + 35\)
- \(x^2 - 15x + 56\)
- \(x^2 - 13x + 40\)
Solutions:
- \(x^2 - 5x + 6 = (x - 3)(x - 2)\)
- \(x^2 - 9x + 20 = (x - 5)(x - 4)\)
- \(x^2 - 7x + 10 = (x - 5)(x - 2)\)
- \(x^2 - 11x + 30 = (x - 6)(x - 5)\)
- \(x^2 - 8x + 15 = (x - 5)(x - 3)\)
- \(x^2 - 10x + 21 = (x - 7)(x - 3)\)
- \(x^2 - 6x + 8 = (x - 4)(x - 2)\)
- \(x^2 - 12x + 35 = (x - 7)(x - 5)\)
- \(x^2 - 15x + 56 = (x - 8)(x - 7)\)
- \(x^2 - 13x + 40 = (x - 8)(x - 5)\)
Remember to always check your results by multiplying the factors. If the product matches the original trinomial, then the factoring is correct.
Factoring Lesson A by ChatGPT-4
Factoring Trinomials of the Form \(x^2 + bx + c\)
Factoring trinomials, which are polynomials with three terms, can initially seem challenging. However, with practice, it becomes routine. If a trinomial factors, it will factor into the product of two binomials.
Steps to Factor Trinomials:
- Factor the first term: \(x^2 = x \cdot x\).
- Factor the last term: Choose factors that add or subtract to obtain the middle term.
- Determine the signs: by adding or subtracting the product of the inner and outer terms.
- Check by multiplying.
Example:
Factor the trinomial \(x^2 + 7x + 12\).
- Factor the first term: \(x^2 = x \cdot x\).
- Factor the last term: \(12 = 3 \cdot 4\) and \(3 + 4 = 7\), which is our middle term.
- Determine the signs: Both signs are positive because \(+3 + 4 = +7\).
- Check by multiplying: \((x + 3)(x + 4) = x^2 + 7x + 12\).
So, \(x^2 + 7x + 12 = (x + 3)(x + 4)\).
Exercises:
Factor the following trinomials:
- \(x^2 + 5x + 6\)
- \(x^2 + 9x + 20\)
- \(x^2 + 7x + 10\)
- \(x^2 + 11x + 30\)
- \(x^2 + 8x + 15\)
- \(x^2 + 10x + 21\)
- \(x^2 + 6x + 8\)
- \(x^2 + 12x + 35\)
- \(x^2 + 15x + 56\)
- \(x^2 + 13x + 40\)
Solutions:
- \(x^2 + 5x + 6 = (x + 3)(x + 2)\)
- \(x^2 + 9x + 20 = (x + 5)(x + 4)\)
- \(x^2 + 7x + 10 = (x + 5)(x + 2)\)
- \(x^2 + 11x + 30 = (x + 6)(x + 5)\)
- \(x^2 + 8x + 15 = (x + 5)(x + 3)\)
- \(x^2 + 10x + 21 = (x + 7)(x + 3)\)
- \(x^2 + 6x + 8 = (x + 4)(x + 2)\)
- \(x^2 + 12x + 35 = (x + 7)(x + 5)\)
- \(x^2 + 15x + 56 = (x + 8)(x + 7)\)
- \(x^2 + 13x + 40 = (x + 8)(x + 5)\)
Remember to always check your results by multiplying the factors. If the product matches the original trinomial, then the factoring is correct.
Comprehensive Algebra Video Guide: Step-by-Step Solutions & Tutorials

1.1 Real Numbers and The Number Line
1.2 Adding and Subtracting Integers
1.3 Multiplying and Dividing Integers
1.4 Fractions
1.5 Review of Decimals and Percents
1.6 Exponents and Square Roots
1.7 Order of Operations
2.1 Introduction to Algebra
2.2 Simplifying Algebraic Expressions
2.3 Linear Equations: Part I
2.4 Linear Equations: Part II
2.5 Applications of Linear Equations
2.6 Ratio and Proportion Applications
2.7 Introduction to Inequalities and Interval Notation
2.8 Linear Inequalities (one variable)
3.1 Rectangular Coordinate System
3.2 Graph by Plotting Points
3.3 Graph using Intercepts
3.4 Graph using the y-intercept and Slope
3.5 Finding Linear Equations
3.6 Parallel and Perpendicular Lines
3.7 Introduction to Functions
3.8 Linear Inequalities (Two Variables)
4.1 Solving Linear Systems by Graphing
4.2 Solving Linear Systems by Substitution
4.3 Solving Linear Systems by Elimination
4.4 Applications of Linear Systems
4.5 Solving Systems of Linear Inequalities (Two Variables)
5.1 Rules of Exponents (Integer Exponents)
5.2 Introduction to Polynomials and Evaluating
5.3 Adding and Subtracting Polynomials
5.4 Multiplying Polynomials and Special Products
5.5 Dividing Polynomials
5.6 Negative Exponents and Scientific Notation
6.1 Introduction to Factoring and Factor by Grouping
6.2 Factoring Trinomials
6.3 Factoring Trinomials ax^2 + bx + c
6.4 Factoring Binomials
6.5 General Guidelines for Factoring Polynomials
6.6 Solving Equations by Factoring
6.7 Applications involving Quadratic Equations
7.1 Simplifying Rational Expressions
7.2 Multiplying and Dividing Rational Expressions
7.3 Adding and Subtracting Rational Expressions
7.4 Complex Fractions
7.5 Solving Rational Equations
7.6 Applications of Rational Equations
7.7 Variation
1 Radicals
2 Simplifying Radical Expressions
3 Adding and Subtracting Radical Expressions
4 Multiplying and Dividing Radical Expressions
5 Rational Exponents
6 Solving Radical Equations