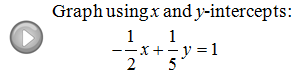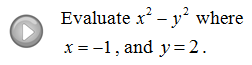Click on a problem to see it worked out in YouTube.
1.1 Real Numbers and The Number Line
1.2 Adding and Subtracting Integers
1.3 Multiplying and Dividing Integers
1.4 Fractions
1.5 Review of Decimals and Percents
1.6 Exponents and Square Roots
1.7 Order of Operations
2.1 Introduction to Algebra
2.2 Simplifying Algebraic Expressions
2.3 Linear Equations: Part I
2.4 Linear Equations: Part II
2.5 Applications of Linear Equations
2.6 Ratio and Proportion Applications
2.7 Introduction to Inequalities and Interval Notation
2.8 Linear Inequalities (one variable)
3.1 Rectangular Coordinate System
3.2 Graph by Plotting Points
3.3 Graph using Intercepts
3.4 Graph using the y-intercept and Slope
3.5 Finding Linear Equations
3.6 Parallel and Perpendicular Lines
3.7 Introduction to Functions
3.8 Linear Inequalities (Two Variables)
4.1 Solving Linear Systems by Graphing
4.2 Solving Linear Systems by Substitution
4.3 Solving Linear Systems by Elimination
4.4 Applications of Linear Systems
4.5 Solving Systems of Linear Inequalities (Two Variables)
5.1 Rules of Exponents (Integer Exponents)
5.2 Introduction to Polynomials and Evaluating
5.3 Adding and Subtracting Polynomials
5.4 Multiplying Polynomials and Special Products
5.5 Dividing Polynomials
5.6 Negative Exponents and Scientific Notation
6.1 Introduction to Factoring and Factor by Grouping
6.2 Factoring Trinomials
6.3 Factoring Trinomials ax^2 + bx + c
6.4 Factoring Binomials
6.5 General Guidelines for Factoring Polynomials
6.6 Solving Equations by Factoring
6.7 Applications involving Quadratic Equations
7.1 Simplifying Rational Expressions
7.2 Multiplying and Dividing Rational Expressions
7.3 Adding and Subtracting Rational Expressions
7.4 Complex Fractions
7.5 Solving Rational Equations
7.6 Applications of Rational Equations
7.7 Variation
1 Radicals
2 Simplifying Radical Expressions
3 Adding and Subtracting Radical Expressions
4 Multiplying and Dividing Radical Expressions
5 Rational Exponents
6 Solving Radical Equations