

[Interactive: Ellipses ]
Given the equation of an ellipse in standard form we can graph it using the following steps:
- First plot the center (h, k).
- Plot a point a units up and down from the center.
- Plot a point b units left and right of the center.
- Sketch the ellipse and label the four points.

In this example the major axis is the vertical axis and the minor axis is the horizontal axis. The major axis measures 2b = 10 units in length and the minor axis measures 2a = 6 units in length. There are no x- and y- intercepts in this example.
Graph the ellipse. Label the center and 4 other points.









It will often be the case that the ellipse is not given in standard form. In this case, we will begin by rewriting it in standard form.
Graph the ellipse. Label the center and four other points.









The next set of examples give the equations in general form. Complete the squares to obtain standard form. Remember to factor the leading coefficient out of each variable grouping before using (B/2)^2 to complete the square.
Graph the ellipse. Label the center and four other points.






Answer the questions.






When the calculation for intercepts yields complex results then there are no real intercepts. This just means that the graph does not cross that particular axis.
Example: Find the equation of the ellipse centered at (3, -1) with a horizontal major axis of length 10 units and vertical minor axis of length 4 units.
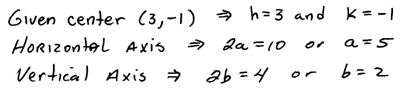


Example: Find the equation of the ellipse given the vertices ( ±3,0) and (0, ±8).

Example: Find the equation of the ellipse whose major axis has vertices (-1, -2) and (-1, 10) and minor axis has co-vertices (-3, 4) and (1, 4).


YouTube Videos:


