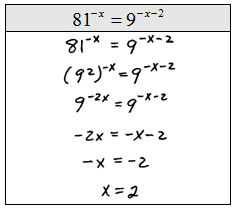Simplifying Radical Expressions

Now when working with square roots and variables we should be a bit careful.

Playlist: Steps for Simplifying Radical Expressions

The variable could represent a positive or negative number so we must ensure that it is positive by making use of the absolute value.

To avoid this technicality many textbooks state, at this point, that we assume all variables are positive. If not, use the absolute values as in the following problems.

Simplify. (Assume variables could be negative.)

To avoid many of the technicalities when working with nth roots we will assume, from this point on, that all the variables are positive.

Simplify. (Assume all variables represent positive numbers.)

Students often try to simplify the previous problem. Be sure to understand what makes the following problems all different.

       

The property:

says that we can simplify when the operation is multiplication.  There is no corresponding property for addition or subtraction.

Video Examples on YouTube:

Solving Exponential Equations

In this section, we will make use of what we have learned about exponential functions to solve equations.

Playlist on Solving Exponential Equations

Make use of the above property if you are able to express both sides of the equation in terms of the same base.

   Step 1: Express both sides in terms of the same base.
   Step 2: Equate the exponents.
   Step 3: Solve the resulting equation.

Solve.

It is not always the case that we will be able to express both sides of an equation in terms of the same base.  For this reason we will make use of the following property.

Make use of the above property if you are unable to express both sides of the equation in terms of the same base.

   Step 1: Isolate the exponential and then apply the logarithm to both sides.
   Step 2: Apply the power rule for logarithms and write the exponent as a factor of the base.
   Step 3: Solve the resulting equation.

Solve.

 

When solving exponential equations and using the above process, the rule of thumb is to choose the common logarithm unless the equation involves the natural base e.   We choose these because there is a button for them on the calculator. However, we could certainly choose any base that we wish; this is the basis for the derivation of the change of base formula.

YouTube Videos: