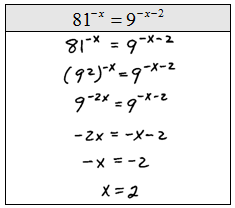Solving Exponential Equations

In this section, we will make use of what we have learned about exponential functions to solve equations.

Playlist on Solving Exponential Equations

Make use of the above property if you are able to express both sides of the equation in terms of the same base.

   Step 1: Express both sides in terms of the same base.
   Step 2: Equate the exponents.
   Step 3: Solve the resulting equation.

Solve.

It is not always the case that we will be able to express both sides of an equation in terms of the same base.  For this reason we will make use of the following property.

Make use of the above property if you are unable to express both sides of the equation in terms of the same base.

   Step 1: Isolate the exponential and then apply the logarithm to both sides.
   Step 2: Apply the power rule for logarithms and write the exponent as a factor of the base.
   Step 3: Solve the resulting equation.

Solve.

 

When solving exponential equations and using the above process, the rule of thumb is to choose the common logarithm unless the equation involves the natural base e.   We choose these because there is a button for them on the calculator. However, we could certainly choose any base that we wish; this is the basis for the derivation of the change of base formula.

YouTube Videos:

Absolute Value Equations

Absolute value, by definition, is the distance from zero on a number line.

How to Solve Absolute Value Equations Playlist

If we have |x| = 3 then the question is, “what number can x be so that the distance to zero is 3?” There are two solutions to this question -3 and 3.

In general,

Here n is a positive integer and X represents an algebraic expression called the argument of the absolute value. To solve these equations, set the argument equal to plus or minus n and solve the resulting equations.

Solve.

This technique requires us to first isolate the absolute value. Apply the usual steps for solving to obtain the absolute value alone on one side of the equation, and then set the argument to plus or minus n.

Solve.

When two absolute values are equal we can set the argument of one equal to the argument of the other.

Tip: When in doubt of a solution, check to see if it solves the original equation.  For example, check that {-7, 3} is the solution set for,

Notice that both numbers solve the original equation and therefore we have verified they are in the solution set.

YouTube Videos: