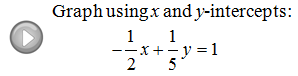The
x-intercept is the point where the graph intersects the
x-axis and the
y-intercept is the point where the graph intersects the
y-axis. These points have the form (
x, 0) and (0,
y) respectively.
To find the
x- and
y-intercepts algebraically, we use the fact that all
x-intercepts have a
y-value of zero and all
y-intercepts have an
x-value of zero. For example,
Graph: 3x − 5y = 15
Tip 1: To find the
y-intercept, set
x = 0 and determine the corresponding
y-value. Similarly, to find the
x-intercept we set
y = 0 and determine the corresponding
x-value.
Keep in mind that the intercepts are ordered pairs and not numbers. In other words, the
x-intercept is not
x = 5 but rather (5, 0).
Two points determine a line. If we find the
x- and
y-intercepts, then we can use them to graph the line. As you can see, they are fairly easy to find. Plot the points and draw a line through them with a straightedge.
Done. Let’s do another one.
Graph: y = −x + 9
We begin by finding the
x-intercept.
The
x-intercept is (3, 0).
The
y-intercept is (0, 9). Now graph the two points.
Tip 2: Use
Desmos.com to check your answer – it’s totally free. Just type in the equation.
This is a nice and easy method for determining the two points you need for graphing a line. In fact, we will use this exact technique for finding intercepts when we study the graphs of all the conic sections later in our study of Algebra.
Graph −4
x + 3
y = 12 using the intercepts.
Graph −4
x + 2
y = −6 using the intercepts.
Graph y = −5x +15 using the intercepts.
Graph y = −3/4
x + 9 using the intercepts.
This brings us to one of the most popular questions in linear graphing. Do all lines have
x- and
y-intercepts? The answer is NO. Horizontal lines, of the form
y =
b, do not necessarily have
x-intercepts. Vertical lines, of the form
x =
a, do not necessarily have
y-intercepts.
Graph y = 3.
Graph x = −2.
Many students this method, but I will tell you, there is a better way. Even less work... [ Graph Lines using Slope and Intercepts ] Read on!
---