
Example: If a $500 certificate of deposit earns 4 1/4% compounded monthly then how much will be accumulated at the end of a 3 year period?
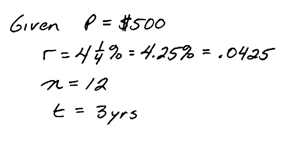

Example: A certain investment earns 8 3/4% compounded quarterly. If $10,000 is invested for 5 years, how much will be in the account at the end of that time period?


The basic idea is to first determine the given information then substitute the appropriate values into the formula and evaluate. To avoid round-off error, use the calculator and round-off only once as the last step.
- Annual n = 1
- Semiannual n = 2
- Quarterly n = 4
- Monthly n = 12
- Daily n = 365
One important application is to determine the doubling time. How long does it take for the principal in an account earning compound interest to double?
Example: How long does it take to double $1000 at an annual interest rate of 6.35% compounded monthly?


The key step in this process is to apply the common logarithm to both sides so that we can apply the power rule and solve for time t. Use the calculator in the last step and round-off only once.
Example: How long will it take $30,000 to accumulate to $110,000 in a trust that earns a 10% return compounded semiannually?


Example: How long will it take our money to triple in a bank account with an annual interest rate of 8.45% compounded annually?


Make a note that doubling or tripling time is independent of the principal. In the previous problem, notice that the principal was not given and that the variable P cancelled.

Example: If a $500 certificate of deposit earns 4 1/4% annual interest compounded continuously then how much will be accumulated at the end of a 3 year period?


Example: A certain investment earns 8 3/4% compounded continuously. If $10,000 dollars is invested, how much will be in the account after 5 years?


The previous two examples are the same examples that we started this chapter with. This allows us to compare the accumulated amounts to that of regular compound interest.




Given continuously compounding interest, we are often asked to find the doubling time. Instead of taking the common log of both sides it will be easier take the natural log of both sides, otherwise the steps are the same.
Example: How long does it take to double $1000 at an annual interest rate of 6.35% compounded continuously?


The key step in this process is to apply the natural logarithm to both sides so that we can apply the power rule and solve for t. Use the calculator in the last step and round-off only once.
Example: How long will it take $30,000 to accumulate to $110,000 in a trust that earns a 10% annual return compounded continuously?


Example: How long will it take our money to triple in a bank account with an annual interest rate of 8.45% compounded continuously?


YouTube Video:
---

