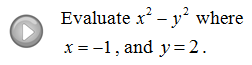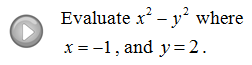Function Composition

Here is where we introduce a new operation - composition of functions.  With this definition comes new notation.

YouTube Playlist Introduction to Functions

This new notation reads “f composed with g.”

The idea is to substitute one function into another function.

Given the functions f(x) = 5x – 4 and g(x) = 2x – 1.

Composition of functions is not necessarily a commutative operation, in other words, order matters.

Given the functions f(x) = x^2 – 9 and g(x) = x – 3.

Given the functions f(x) = x^2 + 1 and g(x) = sqrt(x – 1) where ( x >= 1 ).

At this point we must understand what happens to the domain of a composite function. In the above example it might appear that f o g has a domain of all real numbers.  In fact, the domain is restricted to [1, inf) because that is the domain of g.  The domain of f o g consists of all the values in the domain of g that are also in the domain of f.

Given f and g find f o g and state its domain.

YouTube Videos:

Introduction to Polynomials

Before beginning this section we first make a few definitions. Some of the terms have already been defined but it does not hurt to go over them again. First recall that algebraic expressions such as,

are called terms. The term,

has a coefficient −2 and a variable part a^2 b. A polynomial is any sum or difference of algebraic terms. A polynomial with only one term is called a monomial. A polynomial with 2 terms is called a binomial and one with 3 terms is called a trinomial.  We will not use any other special names for polynomials with more terms.

It is common practice to express polynomials in descending order from largest exponent down to the constant term. The constant term, or the term with no variable part, can be thought of as the coefficient of the x^0 term.

The degree of a polynomial with one variable is the largest exponent.

Evaluating expressions involves replacing the variable with the appropriate numerical value. In other words, plug in the values and use the order of operations to calculate the answer.

Evaluate.

Simplifying expressions first saves steps when evaluating and the results will be the same.

We can use function notation to evaluate. Do not let the notation get in the way of your ability to do these types of problems. The idea is the same, just substitute in the appropriate values.

Evaluate.

We will often run into problems where the graph is given instead of the algebraic equation. In this case, read the graph and answer the question.

Given the graph of the function.

Given the graph of the function.

Projectile Problem: A projectile is fired from the ground with an initial velocity of 64 feet per second. The height of the projectile in feet after t seconds is given by the function

  with the following graph:

   a. Use the graph to determine how much time it takes to reach the maximum height.
   b. How much time will it take to hit the ground?
   c. What times will the projectile be at 60 feet?
   d. Use the function  to determine the height of the projectile at t = 1 second.

Read the graph to answer a, b, and c.

Geometry Problem: The function

gives the volume of a sphere given its radius r. Use the function to calculate the volume of a sphere of radius 6 centimeters. (Use 3.14 as an approximation for pi.)

Projectile Problem: A projectile is fired upwards from the roof of a 256 foot building with an initial velocity of 96 feet per second. The height of the projectile in feet after t seconds is given by

whose graph is given:

   a. How much time does it take to reach a maximum height?
   b. What is the maximum height?
   c. How much time does it take for the projectile to hit the ground?
   d. Use the function to determine the height after 6 seconds.

Read the graph to answer a, b, and c.

Video Examples on YouTube: